Оглавление                                                                                                                                                             Вперёд

Глава 2

ИЗМЕРЕНИЯ ПО КАРТЕ

 

 § 7. ИЗМЕРЕНИЕ РАССТОЯНИЙ И ПЛОЩАДЕЙ

 

1. Масштаб карты

Масштаб карты—одна из важнейших ее характеристик. Он определяет степень уменьшения линий на карте относительно горизонтальных проложений соответствующих им линий на местности.

Масштаб указан на каждом листе карты под южной (нижней) стороной рамки в числовом (численный масштаб) и графическом (линейный масштаб) виде (рис. 11).

Численный масштаб в общем виде, т. е. безотносительно к какой-либо определенной системе линейных мер, обозначается на картах в виде отношения 1 : М, где М - число, указывающее, во сколько раз уменьшены длины линий на местности при изображении их на карте. Так, масштаб 1:50000 означает, что любой единице длины на карте соответствует 50000 таких же единиц на местности.

Для практического использования при измерениях по карте численный масштаб, кроме того, представляют именованным числом, указывая непосредственно величину масштаба, т. е. расстояние на местности, соответствующее 1 см карты. Так, для 1 :50 000 карты величина масштаба равна 500 м.

Отсюда следует, что длина линии на местности равна произведению величины масштаба на длину отрезка (k), измеренную на карте в сантиметрах. Например, отрезку 3,95 см на карте масштаба 1:100000 соответствует на местности расстояние d=1 км ´ 3,95=3,95 км.

Очевидно, что такому же отрезку k, измеренному по карте какого-либо другого масштаба, на местности будет соответствовать расстояние во столько раз больше или меньше указанного, во сколько раз величина масштаба этой карты больше или меньше величины масштаба карты 1 : 100000.

На таком простом соотношении основывается правило устного счета расстояний по величине отрезков, измеренных на топографических картах различных масштабов (табл. 4).

 

 

 

 

 

                                                                                                                                                                                                                                                        

 

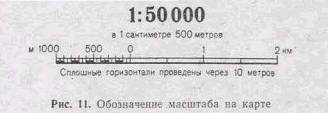
Таблица 4

 

Линейный масштаб представляет собой график, предназначенный для непосредственного отсчета по нему расстояний (в километрах, метрах), измеряемых или откладываемых на карте. Однако в полевых условиях, когда работать приходится на сложенной карте, им пользуются сравнительно редко, а отрезки на карте измеряют с помощью миллиметровой (масштабной) линейки.

 

2. Измерение линий на карте

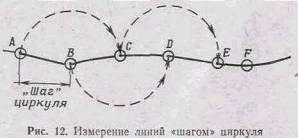
Прямые линии измеряют обычно линейкой. Извилистые и ломаные линии измеряют по частям циркулем-измерителем. Для этого устанавливают по линейке или линейному масштабу раствор циркуля, соответствующий какому-нибудь целому числу километров или сотен метров, и таким «шагом» проходят вдоль измеряемой линии, ведя счет перестановок ножек. Порядок измерения показан на рис. 12, где AF - измеряемая линия, A, В, С, ..., Е места постановки ножек, EF — остаток, измеряемый по линейке (линейному масштабу). Стрелками показано направление перемещения ножек.

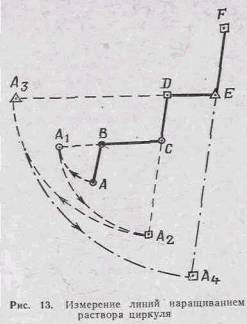
Величину «шага» выбирают, в зависимости от извилистости линии: от 4 - 5 см - при измерении кривых с плавными закруглениями, до 1 - 2 см — при измерении линий с большим числом резких поворотов. Последние более удобно измерять так, как показано на рис. 13. Ломаная ABCDEF равна по длине конечному раствору циркуля A₄F, величину которого определяют по масштабной линейке.

 

 

 

 

 

 

 

 

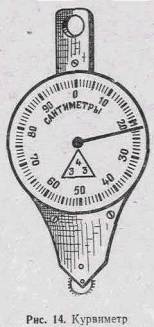
Для измерения кривых и извилистых линий используют также специальный прибор — курвиметр (рис. 14). Механизм этого прибора состоит из измерительного колесика, соединенного системой зубчатых передач со стрелкой, которая движется по циферблату. При движении колесика вдоль измеряемой по карте линии стрелка передвигается по циферблату и указывает пройденное колесиком расстояние в сантиметрах. Для измерения расстояния следует предварительно вращением колесика установить стрелку курвиметра в начальное положение, т. е. на отсчет «0», а затем прокатить его вдоль измеряемой линии, следя за тем, чтобы стрелка двигалась по циферблату в направлении чисел 10, 20 и 30 и т. д. Умножив величину масштаба карты на показание стрелки курвиметра, получают расстояние на местности.

Перед употреблением курвиметр следует проверить, измерив им какую-нибудь линию, длина которой известна, например 10 - 20 см линии километровой сетки.

Для более точного измерения и откладывания расстояний по карте, например при подготовке к ориентированию на местности с помощью навигационной аппаратуры или при определении исходных данных для стрельбы, применяют поперечный масштаб — специальный график, награвированный на металлической. линейке (рис. 15, а). Карта для таких измерений должна быть хорошо расправлена и прикреплена к какой-либо жесткой основе (планшету).

Построение поперечного масштаба основано на пропорциональности отрезков параллельных линии, пересекающих стороны угла

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

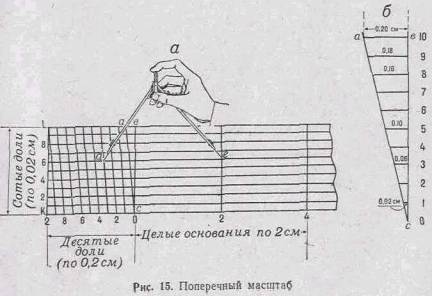
асв (рис. 15, б). Цена наименьшего деления масштаба равна 0,02 см.

Оцифровка делений на масштабе (рис. 15, а) означает: вправо от нуля — число целых оснований масштаба (обычно по 2 см в каждом), влево от нуля—число десятых долей основания, а вверх по линии KL — число сотых долей основания. Важно отметить, что такая оцифровка особенно удобна при измерениях по карте масштаба 1:50000, так как цифры указывают непосредственно расстояния на местности в километрах, сотнях и десятках метров соответственно. При пользовании картами других масштабов надо вначале определить, какому числу метров на местности соответствует основание масштаба, его десятая и сотая доли.

Пользование поперечным масштабом показано на рис. 15, а. Пусть требуется определить расстояние на местности, соответствующее отрезку de на карте масштаба 1:25000. Раствор циркуля, равный этому отрезку, устанавливают на поперечном масштабе так, чтобы, во-первых, обе ножки оказались на одной горизонтальной линии и, во-вторых, правая ножка находилась на одном из перпендикуляров к основанию (точка e), а левая—на одной из наклонных линий (точка d). Для 1:25 000 карты основание масштаба соответствует 500 м, десятая доля основания — 50 м, сотая — 5 м. По цифровым обозначениям линий видно, что этот отрезок  равен 500´1+50´3+5Х´6=680 м.

3. Точность измерения расстояний по карте

Опытным путем установлено, что с помощью циркуля измерения прямолинейных отрезков на карте и других чертежах не могут быть выполнены точнее, чем 0,2 мм. Расстояние на местности, соответствующее 0,2 мм на карте, называют предельной точностью масштаба карты.

Однако точность определения расстояний по карте зависит не только от точности измерений, но и от погрешностей самой карты, неизбежных при ее составлении и печатании, которые могут достигать 0,5 мм, а на картах горных районов - 0,75 мм. Источниками ошибок измерений являются также помятость и деформация бумаги. С учетом этого фактическая точность измерения прямых линий по карте, как показывает практика, колеблется в пределах 0,5 - 1,0 мм, что в масштабе 1:25000 на местности составляет 12 - 25 м, в масштабе 1:50000 — 25 - 50 м, 1:100000 — 50 - 100 м.

4. Поправки в расстояния за наклон и извилистость линий

Измеренное по карте расстояние получается всегда несколько короче действительного. Одна из причин этого состоит в том, что по карте измеряются горизонтальные проложения, в то время как соответствующие им линии на местности наклонные, т. е. длиннее своих горизонтальных проложений (см. рис. 40).

При точных расчетах, например при подготовке данных для стрельбы артиллерии в горной местности, это обстоятельство приходится учитывать и вводить соответствующие поправки как при определении по карте наклонных дальностей, так и при откладывании на ней расстояний, измеренных на местности.

Поправочные коэффициенты для такого перехода приведены в табл. 5.

 

 

Таблица 5

 

Пример 1. По карте определены: расстояние d=3000 м, угол наклона v==18°. Фактическое расстояние на местности равно. D=3000 м ´ 1,05=3150 м.

Пример 2. На местности измерены: длина линии D=3000 м, угол ее наклона к горизонту v=18°. Горизонтальное проложение этой линии на карте равно d=3000 м ´ 0,95=2850 м.

Длина маршрута, измеренная по карте, бывает короче действительной не только вследствие влияния рассмотренной выше причины, но и потому, что в масштабе карты не всегда возможно изобразить все извилины дорог. При составлении карт дороги, как правило, спрямляются, и тем больше, чем мельче масштаб карты. Это особенно заметно на картах горной и холмистой местности.

В табл. 6 приведены поправочные коэффициенты в длины маршрутов, измеренных по карте. Эти коэффициенты установлены опытным путем и учитывают как наклон, так и извилистость дорог.

 

Таблица 6

 

Из таблицы видно, что на равнинной местности длины маршрутов, измеренные по карте, близки к фактическим. В горной же и холмистой местности измеренные по карте расстояния могут существенно отличаться от действительных. Так, например, вместо 200 км, измеренных по карте 1:200000 горного района, фактическая длина маршрута составит 250 км.

5. Простейшие способы измерения площадей по карте

Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки (см. § 8). Каждому квадрату сетки карт масштабов 1 : 10000 — 1 : 50000 на местности соответствует 1 км², масштаба 1:100000 — 4 км², 1:200000 — 16 км².

Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 2—10 мм (в зависимости от масштаба карты и необходимой точности измерений).

Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем — число квадратов, пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.

По картам масштабов 1 : 25 000 и 1 : 50 000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников в (га) указаны на линейке для каждого масштаба карты. Наложив линейку на карту, сравнивают на глаз измеряемую площадь с площадью прямоугольника.

Оглавление         Вперёд