Предыдущая лекция | Содержание | Следующая лекция
Информатика. Лекция №5. Представление чисел в компьютере.

Представление целых чисел в компьютере.



Целые числа являются простейшими числовыми данными, с которыми оперирует ЭВМ. Для целых чисел существуют два представления: беззнаковое (только для неотрицательных целых чисел) и со знаком. Очевидно, что отрицательные числа можно представлять только в знаковом виде. Целые числа в компьютере хранятся в формате с фиксированной запятой.

Представление целых чисел в беззнаковых целых типах.

Для беззнакового представления все разряды ячейки отводятся под представление самого числа. Например, в байте (8 бит) можно представить беззнаковые числа от 0 до 255. Поэтому, если известно, что числовая величина является неотрицательной, то выгоднее рассматривать её как беззнаковую.

Представление целых чисел в знаковых целых типах.

Для представления со знаком самый старший (левый) бит отводится под знак числа, остальные разряды - под само число. Если число положительное, то в знаковый разряд помещается 0, если отрицательное - 1. Например, в байте можно представить знаковые числа от -128 до 127.

Прямой код числа.

Представление числа в привычной форме "знак"-"величина", при которой старший разряд ячейки отводится под знак, а остальные - под запись числа в двоичной системе, называется прямым кодом двоичного числа. Например, прямой код двоичных чисел 1001 и -1001 для 8-разрядной ячейки равен 00001001 и 10001001 соответственно.
Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке машины. Прямой код отрицательного числа отличается от прямого кода соответствующего положительного числа лишь содержимым знакового разряда. Но отрицательные целые числа не представляются в ЭВМ с помощью прямого кода, для их представления используется так называемый дополнительный код.

Дополнительный код числа.

Дополнительный код положительного числа равен прямому коду этого числа. Дополнительный код отрицательного числа m равен 2k-|m|, где k - количество разрядов в ячейке.
Как уже было сказано, при представлении неотрицательных чисел в беззнаковом формате все разряды ячейки отводятся под само число. Например, запись числа 243=11110011 в одном байте при беззнаковом представлении будет выглядеть следующим образом:
1 1 1 1 0 0 1 1

При представлении целых чисел со знаком старший (левый) разряд отводится под знак числа, и под собственно число остаётся на один разряд меньше. Поэтому, если приведённое выше состояние ячейки рассматривать как запись целого числа со знаком, то для компьютера в этой ячейке записано число -13 (243+13=256=28).
Но если это же отрицательное число записать в ячейку из 16-ти разрядов, то содержимое ячейки будет следующим:
1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1
Знаковый разряд
Возникает вопрос: с какой целью отрицательные числа записываются в виде дополнительного кода и как получить дополнительный код отрицательного числа?
Дополнительный код используется для упрощения выполнения арифметических операций. Если бы вычислительная машина работала с прямыми кодами положительных и отрицательных чисел, то при выполнении арифметических операций следовало бы выполнять ряд дополнительных действий. Например, при сложении нужно было бы проверять знаки обоих операндов и определять знак результата. Если знаки одинаковые, то вычисляется сумма операндов и ей присваивается тот же знак. Если знаки разные, то из большего по абсолютной величине числа вычитается меньшее и результату присваивается знак большего числа. То есть при таком представлении чисел (в виде только прямого кода) операция сложения реализуется через достаточно сложный алгоритм. Если же отрицательные числа представлять в виде дополнительного кода, то операция сложения, в том числе и разного знака, сводится к из поразрядному сложению.

Для компьютерного представления целых чисел обычно используется один, два или четыре байта, то есть ячейка памяти будет состоять из восьми, шестнадцати или тридцати двух разрядов соответственно.

Алгоритм получения дополнительного кода отрицательного числа.

Для получения дополнительного k-разрядного кода отрицательного числа необходимо
  1. модуль отрицательного числа представить прямым кодом в k двоичных разрядах;
  2. значение всех бит инвертировать:все нули заменить на единицы, а единицы на нули(таким образом, получается k-разрядный обратный код исходного числа);
  3. к полученному обратному коду прибавить единицу.


Пример:
Получим 8-разрядный дополнительный код числа -52:
00110100 - число |-52|=52 в прямом коде
11001011 - число  -52  в обратном коде
11001100 - число  -52  в дополнительном коде

Можно заметить, что представление целого числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление: 
1100 1100
 С     С

Представление вещественных чисел в компьютере.



Для представления вещественных чисел в современных компьютерах принят способ представления с плавающей запятой. Этот способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Как и для целых чисел, при представлении действительных чисел в компьютере чаще всего используется двоичная система, следовательно, предварительно десятичное число должно быть переведено двоичную систему.

Нормализованная запись числа.

Нормализованная запись отличного от нуля действительного числа - это запись вида a= m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть 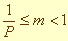. При этом m называется мантиссой числа, q - порядком числа.

Примеры:
  1. 3,1415926 = 0, 31415926 * 101;
  2. 1000=0,1 * 104;
  3. 0,123456789 = 0,123456789 * 100;
  4. 0,00001078 = 0,1078 * 8-4; (порядок записан в 10-й системе)
  5. 1000,00012 = 0, 100000012 * 24.

Так как число ноль не может быть записано в нормализованной форме в том виде, в каком она была определена, то считаем, что нормализованная запись нуля в 10-й системе будет такой:
0 = 0,0 * 100.

Нормализованная экспоненциальная запись числа - это запись вида a= m*Pq, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q - порядком числа.

Представление чисел с плавающей запятой.

При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, был придуман так называемый смещённый порядок, который рассчитывается по формуле 2a-1+ИП, где a - количество разрядов, отводимых под порядок.

Пример:
Если истинный порядок равен -5, тогда смещённый порядок для 4-байтового числа будет равен 127-5=122.

Алгоритм представления числа с плавающей запятой.

  1. Перевести число из p-ичной системы счисления в двоичную;
  2. представить двоичное число в нормализованной экспоненциальной форме;
  3. рассчитать смещённый порядок числа;
  4. разместить знак, порядок и мантиссу в соответствующие разряды сетки.

Пример:
Представить число -25,625 в машинном виде с использованием 4 байтового представления (где 1 бит отводится под знак числа, 8 бит - под смещённый порядок, остальные биты - под мантиссу).



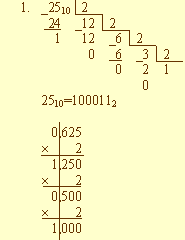
2510=1000112
0,62510=0,1012
-25,62510= -100011,1012
2. -100011,1012 = -1,000111012 * 24
3. СП=127+4=131
4.


Можно заметить, что представление действительного числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:


Окончательный ответ: C1CD0000.
Hosted by uCoz